hex notation shows up a lot in computing so it’s really useful to understand. it’s really hard though to learn to take your base 10 lens off because that’s what we’re so accustom to!
in base 10 position notation, each place represents up to 10 digits (0-9). this is really handy because when we go beyond 9, we can shift over and use a new position to denote 9 + 1. so the value of each position in a base 10 integer is essentially the radix (10) raised to the power of the position index which starts at 0.
for example, the digit symbol 8 below represents the value 8 because every digit is below 10. once you most leftward to a new position, each digit actually represents 10^1 all the way to the leftmost position 10^n.
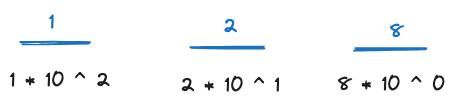
the same set of digits for a base 16 system ends up looking the same, but the actual value is different. below, 128 in base 16 is 296. from right to left, 8 + 32 + 256 = 296. this is because rather than representing 10 symbols in each place, hex holds 16 symbols
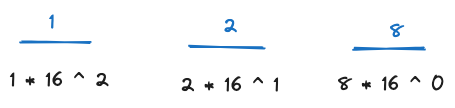
in base 10, each place holds one of 0,1,2,3,4,5,6,7,8,9. in base 16, each place holds one of 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F where A = 10 (base 10), B = 11, C = 12, D = 13, E = 14, F = 15. so A in base 16 is equivalent to 10 in base 10. when looking at this for the first time, it looks wild because you’re so accustomed to equating the symbols “10” with the value “10” (both in base 10), so switching bases really requires you to decouple the numerical symbolic representation (may or may not be base 10) from the value (which you still want to think about and write in terms of base 10).
one of the handiest things about hex and why it’s commonly used in computing is its relationship with binary or base 2 notation. machines encode all information in binary format. compared to decimal and hexadecimal, binary notation only holds 2 values in each positional index (0 and 1). the interesting relationship, though, between binary and hexadecimal is that 16 is actually 2 raised to the 4th power. put another way, we can represent any single hexadecimal value with four binary values and vice versa. this makes converting values between the two bases much easier than converting between binary and base 10. i highly recommend checking out this khan academy video to gain a intuition behind the why
thanks to this relationship, we can use hex as a far more compact literal representation of binary values. while binary is the most efficient for computers, writing in hex makes it far easier to write and read for humans. for example, the bits 1111 can be represented with just F since they both represent the value of 15 (decimal). four bits can represent up to 15 values. what else represents 15 values? a single hexadecimal digit! and since hex is a power of 2, we can expand this beyond just four bits – we can pretty much use hex to quickly convert really any sequence of bits in most computing architectures whether they’re 32bit (8 groups of 4 bits) or 64bit