Isaac Newton came up with an elegant method for calculating square roots through a series of approximations that get refined over time. At the end of this post, I will show a racket implementation of the procedure.
Overview
The square of \(x\) can be written as either \(2*2\) or in the exponential form \(x^2\). Therefore, the square of 2 is 4 because \(2*2\) is 4 and the square of 3 is 9 because \(3 * 3\) is 9. It’s called squaring because when you multiply a number by itself, you form the area of a square since the two numbers are the same and can be conceptualized as equal sides on a square.
Square roots are the inverse of squares and the square root of x can be written in its fractional exponential form \(x ^ {1/2}\) or more commonly \(\sqrt{x}\). If \(\sqrt{x} = y\), then it must also follow that \(y^2 = x\).
A perfect square is a number that is the product of a number multiplied by itself. Some examples of perfect squares are 4 (\(2*2\)), 9 (\(3*3\)), 16 (\(4*4\)), and 25 (\(5*5\)).
Finding the square root by … guessing
What’s the square root of 9? How do you compute this in your head if you don’t already know that the answer is 3?
Start guessing!
Pick a number less than 9 and square it and see how close I get to 9. If the answer is less than 9, then the square root must be larger than my current guess. And if it’s larger than 9, then the square root is smaller than my current guess.
There’s two parts to this process:
- Guessing a number that represents the square root
- Checking whether the square if the guess is within the threshold of what we are looking for (as close to 0 as possible)
To phrase this more precisely, given \(\sqrt{x}\), we’re looking for \(y\) such that \(x – y ^ 2 = 0\).
A closer look at newtons method
\(let\ a = 9\), where 9 is the number we’re trying to find square root for. Think of it as the total area of a rectangle.
\(x\) is our guess.
\(y\) is the other side of our rectangle such as \(x*y = a\)
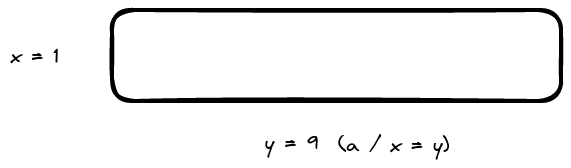
Think of 9 as an area of a rectangle. You can form it in different ways / different dimensions but with the same area. The last shape is a perfect square with equal sides – the side of a perfect square is what we’re looking for.
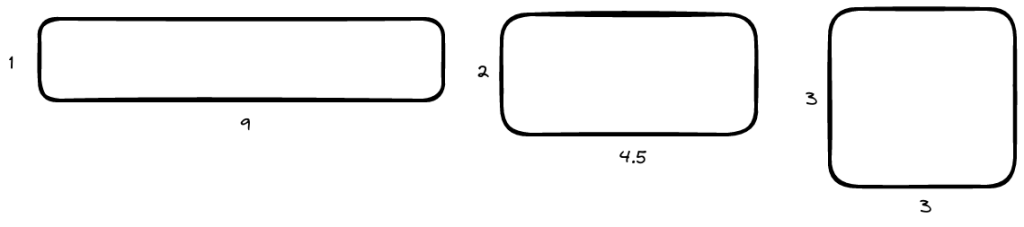
Given any \(x\) and \(y\) such that \(x * y = a\), we know that any other value less than \(x\) if \(y\) is unchanged will be < \(a\) and any value more than \(y\) will be > \(a\).
To make a better guess towards a value that brings us closer to the perfect square such that \(x * y = a\) and \(x = y\), \(x\) needs to be bigger and \(y\) needs to be smaller.
Basically, we want \(x\) to be as close to \(y\) as possible, so they need to get closer over time in order for us to find the answer. Therefore, a better guess needs to be a value that is between \(x\) and \(y\).
One such better guess is the average of \(x\) and \(y\)!
By repeating this process, we converge on the answer.
Racket Implementation
#lang racket
(define (sqrt x)
(define (square x) (* x x))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (average x y) (/ (+ x y) 2))
(define (improve guess x)
(average guess (/ x guess)))
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x) x)))
(sqrt-iter 1.0 x)
)